Equilibrium of the Hip Joint
-
Backround
Analysis of forces in hip joint in static equilibrium is an example of application of principles of mechanics to a biomedical problem. Living systems and structures are much more comlicated than those studied in traditional engineering disciplines. Therefore, many simplifying assumptions are made to render the problem into an engineering one. Many such assumptions are explicitly or implicitly made here as well.
To apply principles of mechanics to the equilibrium of the hip joint, we need to know the forces acting on the hip. There are many muscles attachments around the hip (Hall 2012). However, it is customary to assume that to include the forces applied by hip abductors and ignore the action of other muscles. Hip abductor forces are applied on the greater trochanter of the femur, mainly by gluteus medius accompanied by gluteus minimus and tensor of fascia lata femoris (Okuno & Fratin 2014). Figure 1 illustrates how the hip abductor action is simplified as a single force acting on the greater trochanter. The other end of the main hip abductor, gluteus medius is attached to the iliac crest.
Figure 1 shows that the hip abductor force is applied at angle of 70° The tip of the external force vectors (N, J and H) are placed at their point of application on the leg bones. (Okuno & Fratin 2014, Hall 2012, & Lucas, Cooke & Friis 1999 ).
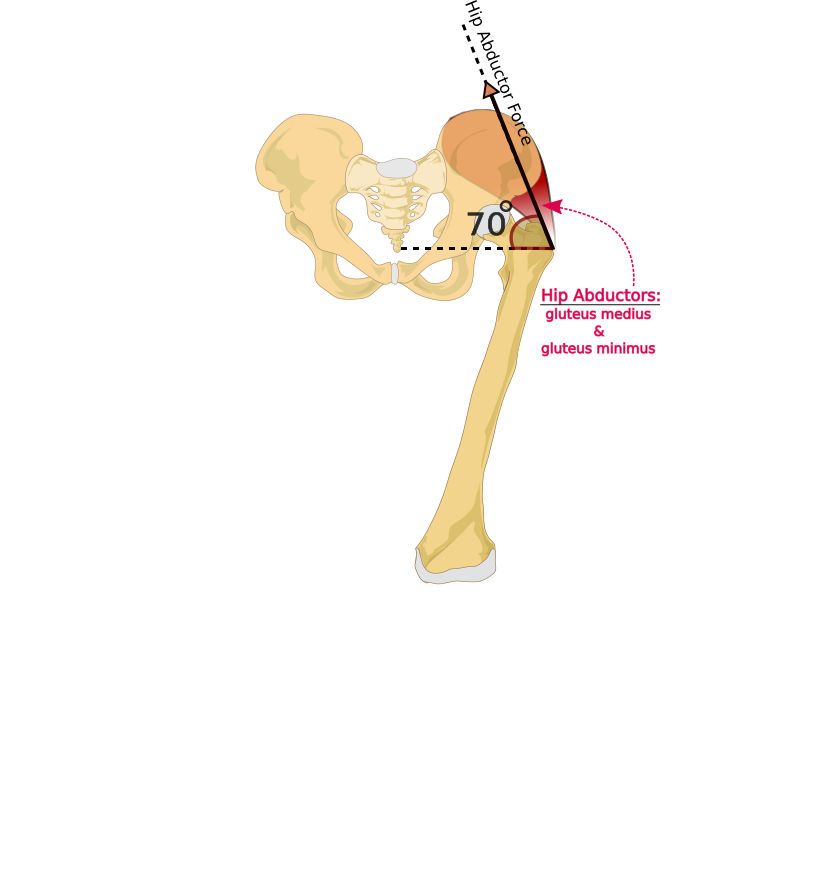
Figure 1. Hip Abductor Force -
Foces Acting on Leg During Standing
Figure 2 shows a Free Body Diagram (FDB) of bones of a left leg of a standing person.
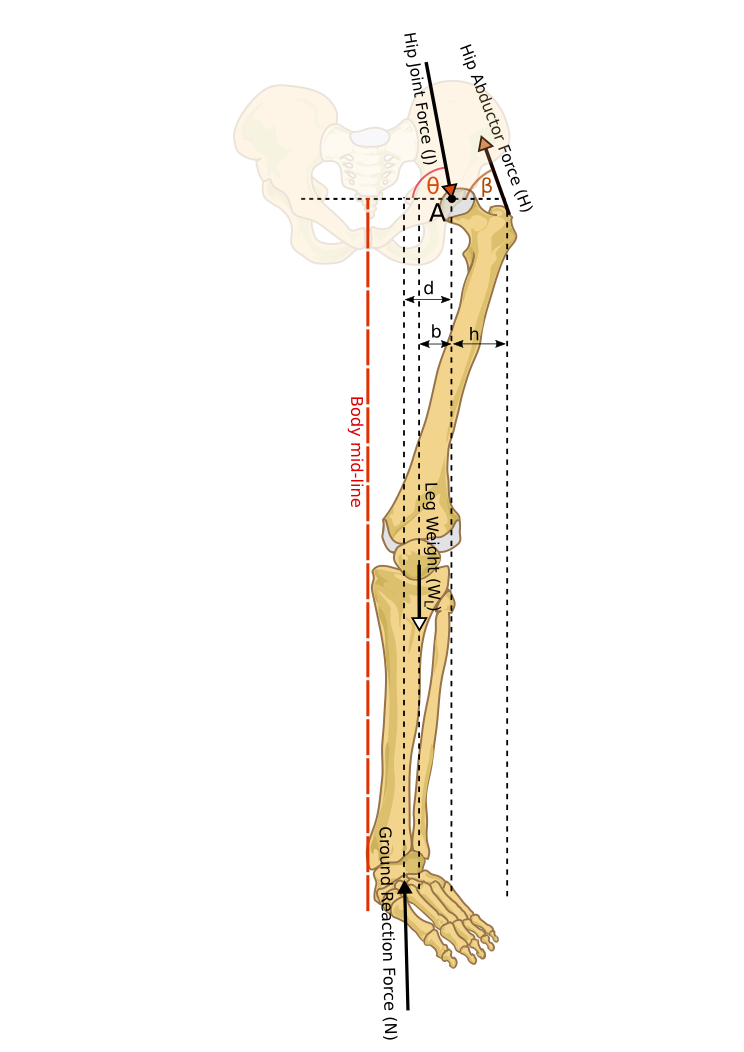
Figure 2. Free Body Diagram of the left leg of a standing person Let us have:
-
: Total Body Weight (TBW)
-
: Weight of the Leg. Usually: , or some times (Okuno & Fratin 2014) (2.1)
-
: Ground Reaction Force (GRF)
-
: Hip Abductor Force (HAF)
-
: Hip Joint Force (HJF)
-
Angle of application of HAF, i.e. β = 70° .(2.2)
From equilibrium of forces in the vertical direction, we can have:
. (2.3)
Balance of forces in the horizontal direction gives:
. (2.4)
Balance of moments around the hip (point A in figure 2) gives:
. (2.5)
Equation (2.5) means: . (2.6)
Substituting from equation (2.6) into equation (2.3) yields: . (2.7)
Substituting from equation (2.6) into equation (2.4) gives: . (2.8)
Equation (2.7) gives the vertical component of , and equation (2.8) gives its horizontal component. They can of course be used to calculate the magnitude of as well.
Dividing each side of equations (2.7) by its corresponding side in equation (2.8) gives:
. (2.9)
About the parameters in equations (2.6) to (2.9):
-
is approximated by equation (2.1).
-
The estimated value for is given in equation (2.2).
-
For the value for the normal GRF, :
In case of two-legged stance the assumption of symmetry gives: , and in case of single-legged stance the fact is that: .
Equation (2.6) to (2.8) can be applied to calculate forces on hip, and , during both two-legged stance and one-legged stance, if , and are given.
-
-
-
References
-
2014 Biomechanics of the Human Body Springer Science+Business Media New York USA ISBN 978-1-4614-8575-9 DOI 10.1007/978-1-4614-8576-6
Section 6.5 Forces on the Hip p106
-
2011 Theoretical Biomechanics InTech Rijeka, Croatia ISBN 978-953-307-851-9
Chapter 11 Estimating Lower Limb Skeletal Loading p243
-
2012 Basic Biomechanics of the Musculoskeletal System 4th Edition Lippincott Williams & Wilkins Baltimore, USA ISBN 978-1-60913-335-1
-
1999 A Primer of Biomechanics Springer Science+Business Media, LLC ISBN 978-0-387-98456-8 DOI 10.1007/978-1-4419-8487-6
Section 2.3 Hip Forces p30
-
2012 Basic Biomechanics 6th Edition McGraw-Hill New York USA ISBN 13: 978-0-07-337644-8
-
2015 Orthopaedic Biomechanics Made Easy Cambridge University Press UK 978-1-107-68546-8
Chapter 6 Biomechanics of the hip and total hip replacement
-