Finite Element Method
A Brief Non-technical Introduction
What is Finite Element Method (FEM)?
FEM is a comutational method for approximate solution of engineering and physical problems
Why approximate solution?
Simply because general and exact solutions only exist for simple geometrical shapes and material behaviours while real world applications have complex physical shapes and properties
Applications of FEM
-
Mechanics: Solids, Fluids and Thermo-mechanics
-
Civil, Structures and Geotechnics
-
Biomechanics
-
Electromagnetics
-
Finance
How it works? (I)
Meshing
→

The geometric shapes of the objects (domain of the problem) is divided into a FINITE number of small and well-defined ELEMENTs.
Elements will have EDGES (sides) and NODES (vertices)
How it works? (II)
Shape Function is Defined
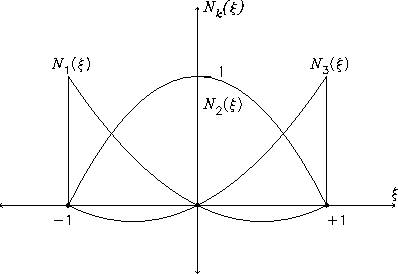
A relation to relate the quantities inside the element to those quantities at the nodes are defined (SHAPE FUNCTION)
How it works? (III)
Deriving Constitutive Matrices of Elements

-
This local (e.g. stiffness) matrix defines the physical behaviour of its ELEMENT
-
It relates the involving quantities (e.g. displacement and loads) to those values at the nodes of the elements
How it works? (IV)
Assembling Global Matrix
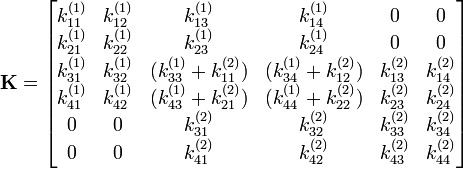
-
Element matrices will be assembled (if time is not involved) into a global matrix for all the elements
-
Transformation of coordinates from local to global is used for assembling
How it works? (V)
Applying Boundary Conditions
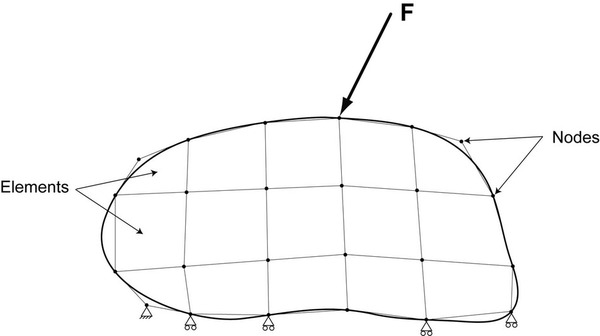
-
Boundary Conditions (BCs) are applied at nodes
-
Global stiffness matrix is modified accordingly
How it works? (VI)
Solving Global Matrix Equation

Global Stiffness × unkowns = Loads
-
The global matrix equation is solved using comutational linear algebra (libraries) giving values at the nodes
-
Shape functions are used to determine values throughout elements
Considerations
-
Convergence
-
Stability
-
Efficiency